Математика в ставках на спорт: теория вероятностей

Математика в ставках имеет решающее значение. На этой точной науке построен весь букмекерский бизнес. Нельзя получить прибыль, надеясь лишь на свои догадки, внутреннее чутьё. Понимание этой концепции отличает победителя от неудачника, успешного игрока от минусового, который регулярно проигрывает свои сбережения в букмекерской конторе. Большинство любителей спортивных пари теряют деньги, а ведь совсем не сложно выделить немного времени и разобраться с основными математическими понятиями в ставках на спорт. Если хотите влиться в ряды плюсовых беттеров, получив знания о том, как работает математика в спортивных ставках, то данная статья поможет вам в этом.

Теория вероятностей

Начнём разбор этой интересной темы с общих понятий. Первый вопрос, который имеет отношение к теории вероятностей – букмекерские коэффициенты. Эти числа должны отражать вероятность того или иного события: победы, тотала, форы. Как рассчитать вероятность с помощью букмекерского коэффициента? Очень просто, нужно разделить единицу на выставленный коэффициент:

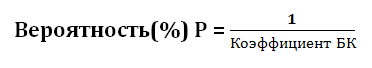
Для примера возьмём матч английской Премьер-лиги между Арсеналом и Манчестер Юнайтед. Букмекер выставил следующие котировки на этот поединок: победа Арсенала 2,05; ничья 3,60; победа МЮ – 3,80. Производим поиск вероятностей всех трёх событий и получаем: виктория Арсенала вероятна на 49%, вничью команды сыграют с вероятностью 28%, Манчестер имеет лишь 26% шансов на успех. В идеале эта сумма должна составлять 100%, но сложив все три числа, получим 103%. Лишние в данном случае 3% — это процент букмекера, или маржа, которую он берёт за свои услуги. 3 процента — это маленькая маржа. Букмекер делает её такой, чтобы завлечь больший поток ставок на топовые встречи. На менее популярные матчи и у более «скупых» контор маржа может достигать 8 процентов и более. Отняв процент маржи, получим истинное значение: 48% — 27% — 25%. Пересчитав полученные данные в коэффициенты при помощи обратной формулы, видим: 2,08 – 3,70 – 4.

Некоторые люди утверждают, что нельзя получить прибыль посредством ставок, так как весь профит уйдёт на маржу. Но это было бы верно в том случае, если бы букмекерские коэффициенты были реальным отражением вероятности события. К счастью для беттеров, никто не может со стопроцентной точность предсказать исход будущего поединка, даже букмекер. Тем более конторы допускают ошибки сознательно, уменьшая маржу на «громких» матчах, а в непопулярных чемпионатах выставляют котировки, исходя только из статистики и не учитывая других важных факторов, которые влияют на мотивацию и саму игру. Такие недооценённые ставки называются валуйными (от англ. Value bet – ценная ставка). Успешный поиск валуйных пари и есть целью для преуспевающего игрока.

Как же математика в спортивных ставках поможет определить, является ли ваш выбор ценным? Это второй вопрос, имеющий отношение к теории вероятностей. Для этого нужно оценить собственную вероятность события и перевести ее в коэффициент. Если он получится ниже, чем кэф букмекера, значит это валуй.

Чтобы определить шансы на событие, обращаемся к статистике. Если хотим узнать шансы на победу гостей, учитываем процент побед на выезде и количество домашних поражений хозяев. Определяем среднее арифметическое, и получаем шансы на П2 в процентах. Затем делим 100 на полученный результат и получаем свой коэффициент.

В качестве примера рассмотрим поединок испанской Ла Лиги Леганес – Бетис. Коэффициент на победу хозяев 1,65; ничья котируется за 3,8; на гостей можно поставить за 5,2. Проводим предматчевый анализ, и получаем следующие вероятности: победа Леганеса 45%, ничья 25%, победа Бетиса 30%. Рассчитаем валуйность для каждого выбора:

П1: 100/45 = 2,2 > 1.65

 Х: 100/25 = 4 > 3,8

 П2: 100/30 = 3,3 < 5,2

Как видно, букмекер недооценил возможную победу гостей, и котировка на этот исход является валуйной.

Третий вопрос, даже догма, которую должен усвоить любой клиент букмекерской конторы – финансовая математика. В качестве опыта возьмём монету и будем подбрасывать её, фиксируя результаты. Очевидно, что при идеальных условиях вероятность, или другими словами математическое ожидание, выпадения орла или решки составляет 50 процентов. Но при малом количестве испытаний результаты могут кардинально отличаться от ожидаемых. Если подбросить монету десять раз, то возможен и такой вариант, что во всех десяти опытах выпадет решка. Такое неравномерное распределение называется дисперсией. При ста испытаниях такое уже невозможно, количество выпавших решек будет в пределах от 40 до 60. Если осуществить 1000 бросков, дисперсия сгладится ещё больше – получим от 440 до 560 решек. Для получения 50 процентов решек необходимо провести бесконечное количество опытов.

Причём здесь финансовая математика и в чём ценность этого примера для беттера? Всё дело в дисперсии. Именно эта коварная закономерность может легко уничтожить игровой банк при неправильном менеджменте и выделении слишком большой суммы на одну ставку. Неудачная полоса даже из пяти минусов в ряд обнулит ваш аккаунт, если позволять себе заключать одно пари на 20 процентов от банкролла. Поэтому крайне важно рисковать не более 1-2% на отдельно взятой ставке. Также необходимо уяснить, что ставки – это долгосрочная инвестиция, а не быстрый заработок. При малом количестве заключенных сделок из-за дисперсии даже опытный и успешный беттер  может оказаться в минусе, а новичок поймать серию побед и возомнить себя гуру в беттинге. Но только дистанция покажет кто есть кто. Прояснить ситуацию о ваших способностях в этой сфере поможет выборка в 500, а лучше в 1000 ставок.

Метод Монте-Карло

Математика в ставках проявляется не только в поиске ценных предложений. Есть также некоторые вспомогательные способы, позволяющие увеличить шансы на успех. Первый из них – метод Монте-Карло, разработанный в прошлом веке Станиславом Уламом. Принцип данной методики – получение множества результатов, которые напрямую зависят от исходных данных. Любой входной параметр, который не может быть установлен точно, представлен в виде большого количества вариантов. После обработки в результате получим набор всех возможных исходов с соответствующими им вероятностями.

Для большей ясности в качестве иллюстрации возьмём гипотетическую ситуацию в чемпионате Испании по футболу, где за чемпионство сражаются Барселона, Реал и Валенсия. До конца первенства 7 туров, клуб из Барселоны является лидером, валенсийцы вторые, мадридцы занимают третье место. Требуется узнать, каковы шансы Валенсии на золотые медали. Снова нам поможет математика в ставках на спорт. Метод Монте-Карло позволит скомпилировать все возможные результаты за оставшиеся туры. Чем качественнее и обширнее входные данные – сведенья о форме команд, индивидуальном мастерстве исполнителей, травмах ключевых игроков и так далее, тем точнее будет результат. Все параметры можно записать в форме пропорций. Допустим, ситуацию с составами и травмами можно выразить как 1:2:3. То есть первая команда играет оптимальным набором игроков и ей отдаётся преимущество, а третья значительно пострадала от различных повреждений. Сгенерировав все, возможные варианты, узнаем примерные шансы валенсийцев на первое место.

Цепь Маркова

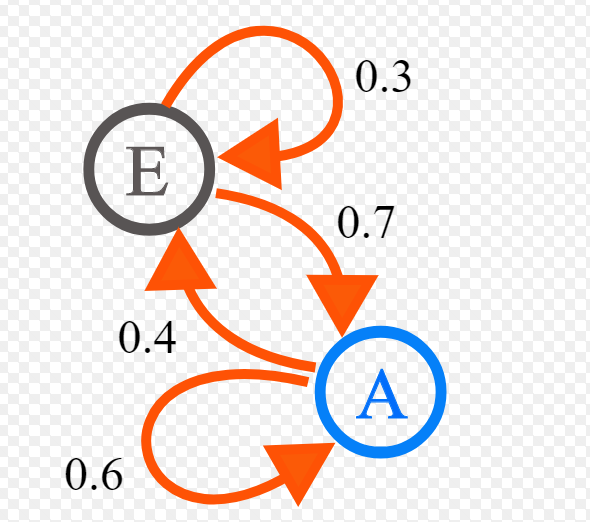
Второй инструмент, на основе которого строится математика в спортивных ставках – цепь Маркова. Этот подход гласит, что вероятность будущего зависит только от того, что есть в данный момент, прошлое никак не может повлиять на возможный исход. Если сказать словами из мира беттинга, то это значит, что любой матч индивидуален. И? к примеру, результат нынешней встречи Спартак – Зенит совершенно не будет зависеть от тех поединков, которые команды сыграли два или три года назад. Необходимо учитывать только текущее положение дел – форму, мотивацию, составы, погоду и так далее. Для анализа важны лишь поединки команд за последние две-три недели или календарный месяц. Финансовая математика игрока будет показывать только тенденцию к росту банка, если грамотно внедрить систему Маркова.

Байесовская вероятность

Два столетия назад Томом Байесом была разработана теория, которая имеет актуальность для беттеров и по сей день. Байесовский принцип гласит: новые обстоятельства влияют на вероятность того или иного исхода. Его можно записать в виде формулы:

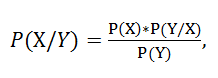
где:

P(X/Y) – вероятность события Х при условии Y;

P(X) – вероятность события Х;

P(Y/X) – вероятность события Y при условии события Х;

P(Y) – вероятность события Y.

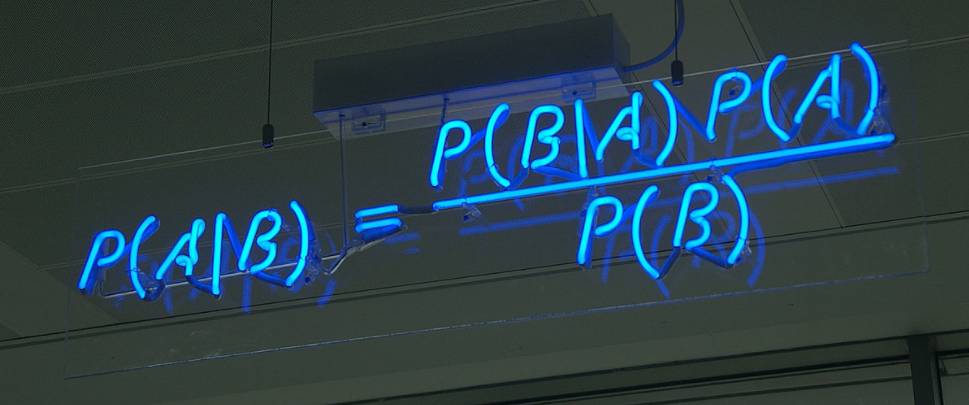
К примеру, интересно ли вам, как погода влияет на коэффициенты на поединок с участием любимого клуба? Снова нам поможет математика в ставках, а именно созданная Байесом теория. Букмекер оценивает шансы на победу ваших любимцев с вероятностью 60%. В 20% победных встреч вашей команды шёл дождь, а средняя вероятность осадков во время поединков 25%. Проведём расчет:

P(X/Y)=(60*25)/20=75%

То есть, вероятность победы ваших любимцев в дождливую погоду составляет 75 процентов.

Математика в ставках, и в частности финансовая математика, являются основой беттинга, и об этом нужно помнить всегда, даже если у вас затянувшаяся чёрная полоса. Знайте – дистанция сгладит дисперсию, и на первое место выйдет ваше мастерство. А увеличить шансы на успех помогут метод Монте-Карло, цепь Маркова и Байесовская вероятность.

Интересно

Виды ставок в кибер баскетболе: от теории к практике за 10 минут

Шорт-хоккей Лига Про: суть турнира, правила и особенности ставок